7 algoritmi, mida iga programmeerija peaks teadma

Programmeerimisüliõpilasena olete tõenäoliselt oma karjääri jooksul õppinud palju erinevaid algoritme. Erinevate algoritmide valdamine on iga programmeerija jaoks hädavajalik.

Nii paljude algoritmide korral võib oluliste asjade jälgimine olla keeruline. Kui valmistute intervjuuks või lihtsalt täiendate oma oskusi, muudab see nimekiri selle suhteliselt lihtsaks. Lugege edasi, kui loetleme programmeerijate jaoks kõige olulisemad algoritmid.

1. Dijkstra algoritm

Edsger Dijkstra oli oma aja üks mõjukamaid arvutiteadlasi ja andis oma panuse palju erinevaid arvutiteaduse valdkondi, sealhulgas operatsioonisüsteemid, kompilaatorite ehitamine ja palju muud rohkem. Üks Dijkstra silmapaistvamaid panuseid on tema lühima graafikute algoritmi leidlikkus, mida tuntakse ka kui Dijkstra lühima tee algoritmi.

Dijkstra algoritm leiab graafiku lühima tee allikast kõigi graafi tippudeni. Igale algoritmi iteratsioonile lisatakse tipp, mille kaugus allikast on minimaalne ja mis puudub praegusel lühimal teel. See on ahne omadus, mida kasutab Djikstra algoritm.

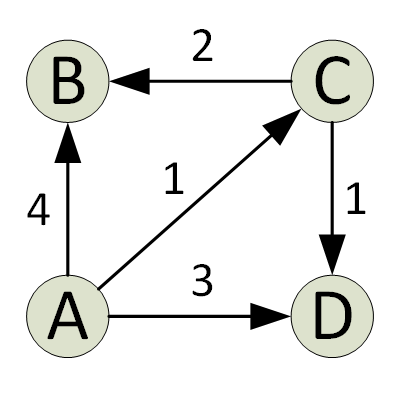
Algoritmi rakendatakse tavaliselt komplekti abil. Dijkstra algoritm on minimaalse hunnikuga rakendamisel väga tõhus; lühima tee leiate vaid O (V+ElogV) ajaga (V on tippude arv ja E on antud graafi servade arv).

Dijkstra algoritmil on oma piirangud; see töötab ainult suunatud ja suunamata graafikutel, mille servad on positiivsed. Negatiivse kaalu puhul on tavaliselt eelistatav Bellman-Fordi algoritm.

Intervjuuküsimused sisaldavad tavaliselt Djikstra algoritmi, seega soovitame tungivalt mõista selle keerukaid üksikasju ja rakendusi.

2. Ühenda Sort

Selles loendis on meil paar sortimisalgoritmi ja ühendamise sortimine on üks olulisemaid algoritme. See on tõhus sorteerimisalgoritm, mis põhineb programmeerimistehnikal Divide and Conquer. Halvimal juhul saab ühendamisjärjekorras sortida „n” numbreid vaid O (nlogn) aja jooksul. Võrreldes primitiivsete sortimistehnikatega nagu Mullide sortimine (see võtab aega O (n^2)), ühendamise sort on suurepäraselt tõhus.

Seotud: Sissejuhatus sorteerimisalgoritmi

Ühendamise korral jagatakse sorteeritav massiiv korduvalt alammassiivideks, kuni iga alammassiiv koosneb ühest numbrist. Seejärel liidab rekursiivne algoritm korduvalt alammassiive ja sorteerib massiivi.

3. Kiire sortimine

Quicksort on veel üks sortimisalgoritm, mis põhineb programmeerimistehnikal Divide and Conquer. Selles algoritmis valitakse esmalt pöördeks element ja kogu massiiv jaotatakse selle pöörde ümber.

Nagu te arvatavasti arvasite, on tõhus pöörde tegemiseks ülioluline hea pöördepunkt. Pivot võib olla juhuslik element, meediumielement, esimene element või isegi viimane element.

Kiirvaliku rakendused erinevad sageli pöördvõtte valimise viisist. Keskmisel juhul sorteerib quicksort suure massiivi koos hea pöördega vaid O (nlogn) ajaga.

Kiirkorralduse üldine pseudokood jaotab massiivi korduvalt liigendil ja paigutab selle alammassiivi õigesse kohta. See asetab ka vasakpoolsest pöördest väiksemad elemendid ja paremale pöördest suuremad elemendid.

4. Esimene sügavus

Depth First Search (DFS) on üks esimesi graafikute algoritme, mida õpilastele õpetatakse. DFS on tõhus algoritm, mida kasutatakse graafiku läbimiseks või otsimiseks. Seda saab muuta ka puude läbimiseks.

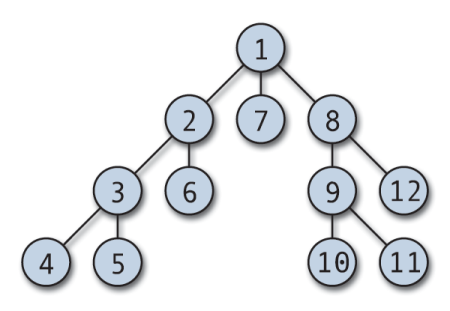
DFS -i läbimine võib alata mis tahes suvalisest sõlmest ja see sukeldub igasse külgnevasse tippu. Algoritm läheb tagasi, kui külastamata tippu pole või on ummiktee. DFS -i rakendatakse tavaliselt virna ja loogilise massiiviga, et jälgida külastatud sõlme. DFS on lihtne rakendada ja erakordselt tõhus; see töötab (V+E), kus V on tippude arv ja E on servade arv.

DFS -i läbimise tüüpilised rakendused hõlmavad topoloogilist sorteerimist, tsüklite tuvastamist graafikus, raja leidmist ja tugevalt ühendatud komponentide leidmist.

5. Laiuse esimene otsing

Breadth-First Search (BFS) on tuntud ka kui puude tasemekorraldus. BFS töötab O (V+E) sarnaselt DFS algoritmile. BFS kasutab aga virna asemel järjekorda. DFS sukeldub graafikusse, samas kui BFS läbib graafi laiuselt.

BFS -i algoritm kasutab tippude jälgimiseks järjekorda. Külastatakse külgnevaid tippe, märgitakse need ja pannakse järjekorda. Kui tipul pole kõrvuti asetsevat tippu, eemaldatakse tipp järjekorrast ja uuritakse seda.

BFS-i kasutatakse tavaliselt võrdõigusvõrkudes, kaalumata graafiku lühimal teel ja minimaalse kattepuu leidmiseks.

6. Binaarotsing

Binaarotsing on lihtne algoritm sorteeritud massiivist vajaliku elemendi leidmiseks. See toimib, jagades massiivi korduvalt pooleks. Kui nõutav element on keskmisest elemendist väiksem, töödeldakse keskmise elemendi vasakut külge edasi; muidu poolitatakse parem pool ja otsitakse uuesti. Protsessi korratakse, kuni vajalik element on leitud.

Binaarotsingu halvim ajaline keerukus on O (logn), mis muudab selle lineaarsete massiivide otsimisel väga tõhusaks.

7. Minimaalsed ulatuspuude algoritmid

Graafiku minimaalse ulatusega puul (MST) on minimaalne kulu kõigi võimalike ulatuspuude hulgas. Laiendava puu maksumus sõltub selle servade kaalust. Oluline on märkida, et minimaalse ulatusega puid võib olla rohkem kui üks. On kaks peamist MST algoritmi, nimelt Kruskal ja Prim.

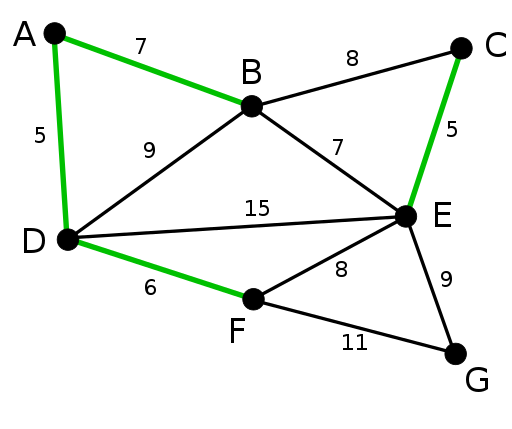
Kruskali algoritm loob MST, lisades kasvavale komplektile serva minimaalsete kuludega. Algoritm sorteerib servad kõigepealt nende kaalu järgi ja lisab seejärel servad MST -le alates miinimumist.

Oluline on märkida, et algoritm ei lisa tsükli moodustavaid servi. Hõredate graafikute puhul eelistatakse Kruskali algoritmi.

Prim'i algoritm kasutab ka ahne omadust ja sobib ideaalselt tihedate graafikute jaoks. Prim'i MST keskne idee on omada kahte erinevat tippude komplekti; üks komplekt sisaldab kasvavat MST -d, teine ​​aga kasutamata tippe. Igal kordamisel valitakse minimaalne kaal, mis ühendab neid kahte komplekti.

Minimaalsed haardepuu algoritmid on klastrianalüüsi, taksonoomia ja levivõrkude jaoks hädavajalikud.

Tõhus programmeerija valdab algoritme

Programmeerijad õpivad ja arendavad pidevalt oma oskusi ning on olemas mõned põhilised põhitõed, mida igaüks peab valdama. Osav programmeerija teab erinevaid algoritme, nende eeliseid ja puudusi ning milline algoritm oleks antud stsenaariumi jaoks kõige sobivam.

Shelli sortimisalgoritmi sissejuhatus

Kuigi kestade sortimine pole kõige tõhusam meetod, on algajatel selle harjutamisest palju kasu.

Loe edasi

Autori kohta